Fuzzy Logic Example
This example is taken from the second edition of the “Artificial Intelligence: A Guide to Intelligent Systems” book by Michael Negnevistky.
The problem is to estimate the level of risk involved in a software engineering project. For the sake of simplicity we will arrive at our conclusion based on two inputs: project funding and project staffing.
Step 1
The first step to convert the crisp input into a fuzzy one. Since we have two inputs we will have 2 crisp values to convert. The first value the level of project staffing. The second value is the level of project funding.
Suppose our our inputs are project_funding = 35% and project_staffing = 60%. We can an get the fuzzy values for these crisp values by using the membership functions of the appropriate sets. The sets defined for project_funding are inadequate, marginal and adequate. The sets defined for project_staffing are small and large.
Thus we have the following fuzzy values for project_funding:
$$ \mu_{\text{funding}=\text{inadequate}}(35) = 0.5 $$
$$\mu_{\text{funding}=\text{marginal}}(35) = 0.2$$
$$\mu_{\text{funding}=\text{adequate}}(35) = 0.0$$
The following a visual representation of this procedure:
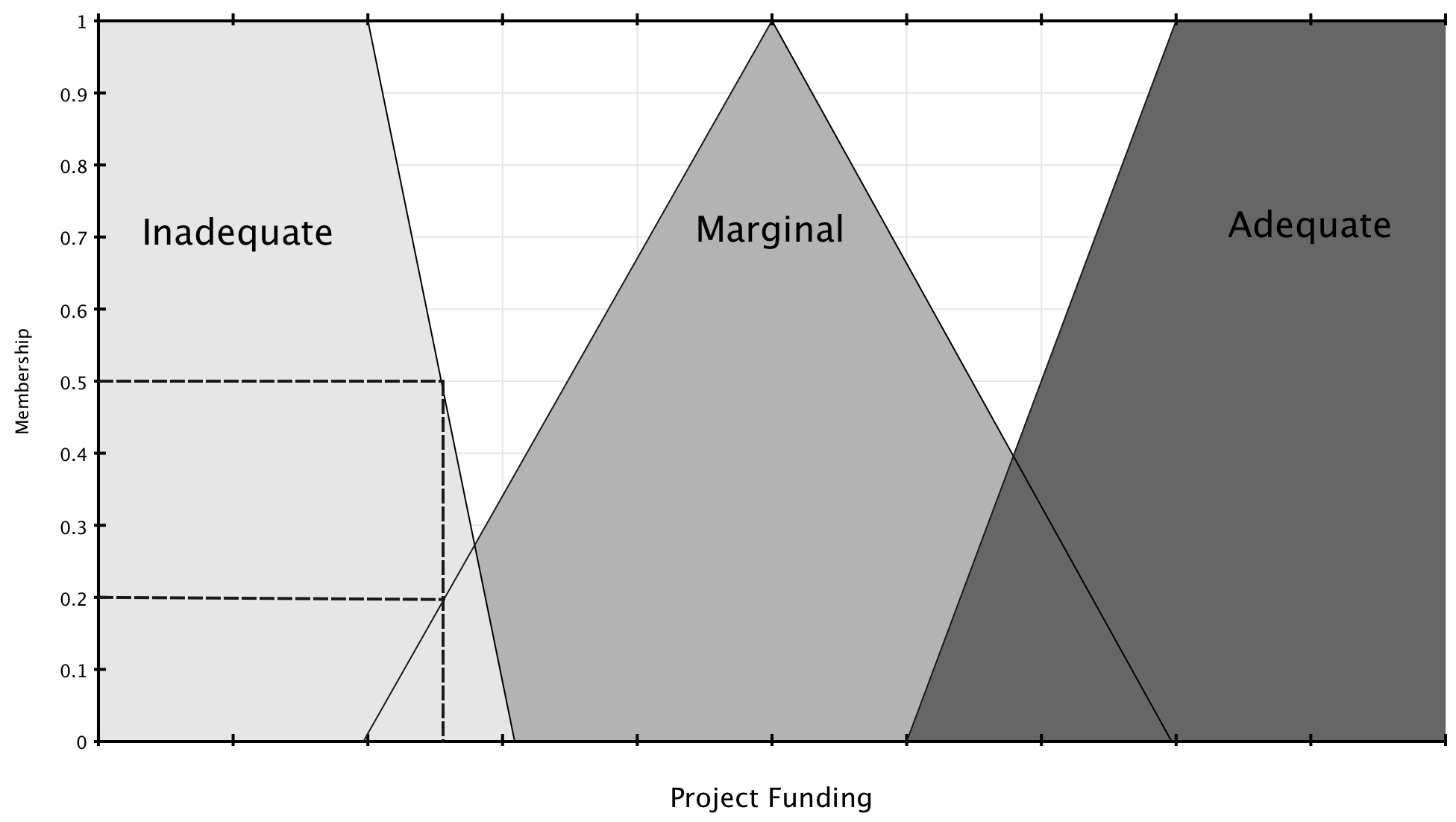
The fuzzy values for project_staffing are shown below.
$$\mu_{\text{staffing}=\text{small}}(60) = 0.1$$
$$\mu_{\text{staffing}=\text{large}}(60) = 0.7$$
The following is a visual representation of this procedure:
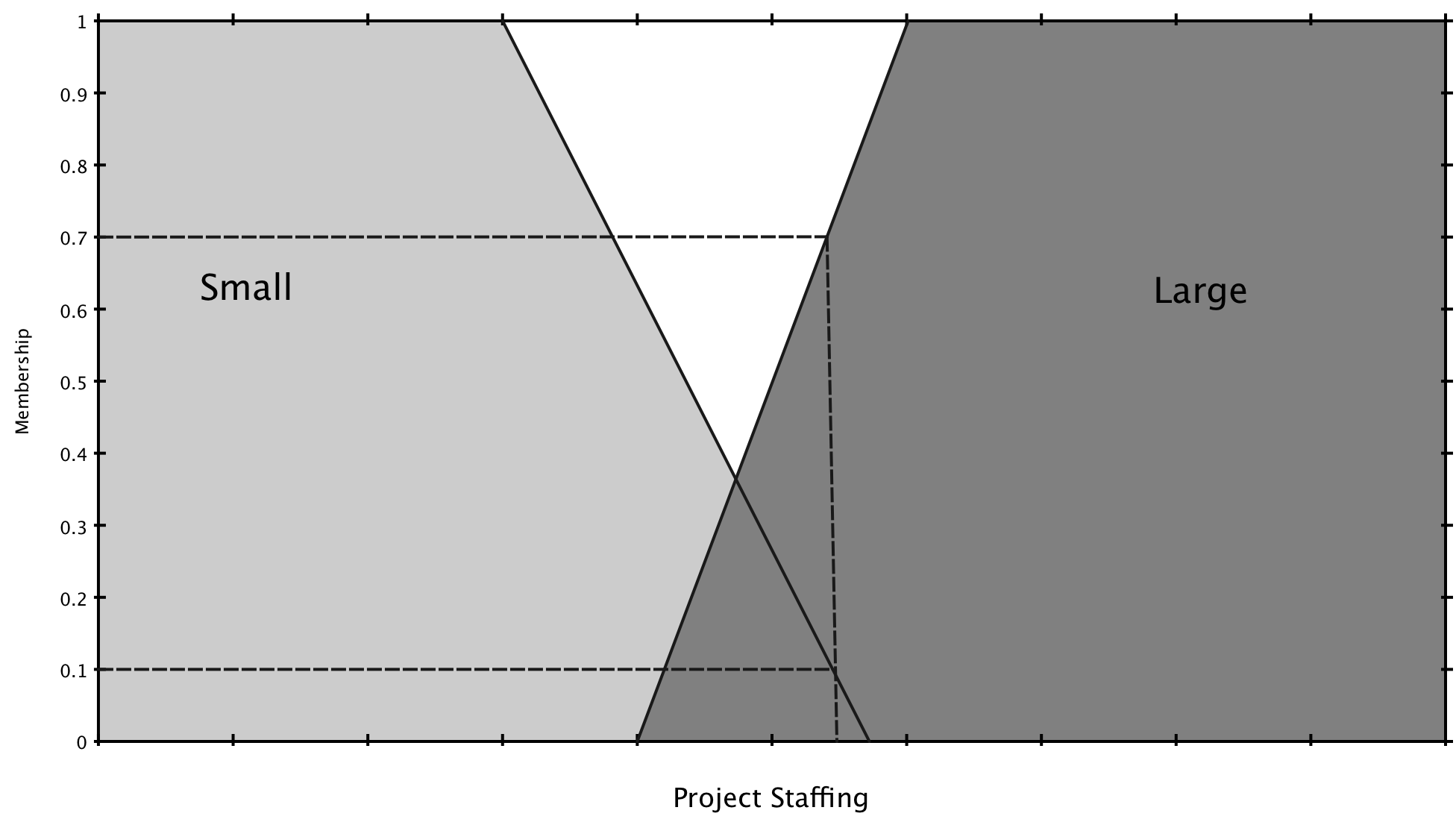
The Rules
Now that we have the fuzzy values we can use the fuzzy rules to arrive at the final fuzzy value. The rules are as follows:
- If
project_fundingis adequate orproject_staffingis small then risk is low. - If
project_fundingis marginal andproject_staffingis large then risk is normal. - If
project_fundingis inadequate then risk is high.
Rule 1 - If project_funding is adequate or project_staffing is small then risk is low
Rules containing disjunctions, OR, are evaluated using the UNION operator.
$$\mu_{A \cup B}(x) = max[\mu_A(x), \mu_B(x)]$$
$$\mu_{\text{risk} = \text{low}} = max[\mu_{\text{funding}=\text{adequate}}(35), \mu_{\text{staffing}=\text{small}}(60)] = max[0.0, 0.1] = 0.1$$
And alternative way of computing the disjunction is via the algebraic sum as shown below:
$$\mu_{A \cup B}(x) = \mu_A(x) + \mu_B(x) - \mu_A(x) * \mu_B(x)$$
$$\mu_{\text{risk} = \text{low}} = 0.0 + 0.1 - 0.0 * 0.1 = 0.1$$
Rule 2 - If project_funding is marginal and project_staffing is large then risk is normal
Conjunctions in fuzzy rules are evaluated using the INTERSECTION operator.
$$\mu_{A \cap B}(x) = min[\mu_A(x), \mu_B(x)]$$
$$\mu_{\text{risk} = \text{normal}} = max[\mu_{\text{funding}=\text{marginal}}(35), \mu_{\text{staffing}=\text{large}}(60)] = max[0.2, 0.7] = 0.2$$
Alternatively the same rule can be evaluated using multiplication, as shown below:
$$\mu_{A \cap B}(x) = \mu_A(x) * \mu_B(x)$$ $$\mu_{\text{risk} = \text{normal}} = 0.2 * 0.7 = 0.14$$
Rule 3 - If project_funding is inadequate then risk is high
$$\mu_{\text{risk} = \text{normal}} = 0.2 * 0.7 = 0.14$$
Rule Evaluation Results
The result of evaluating the rules is shown below:
$$\mu_{\text{risk}=\text{low}}(z) = 0.1$$ $$\mu_{\text{risk}=\text{normal}}(z) = 0.2$$ $$\mu_{\text{risk}=\text{high}}(z) = 0.5$$
We now use the results to scale or clip the consequent membership functions. Once again for the sake of simplicity we will clip each of the functions.
$$\mu_{\text{risk}=\text{low}}(z) = 0.1$$
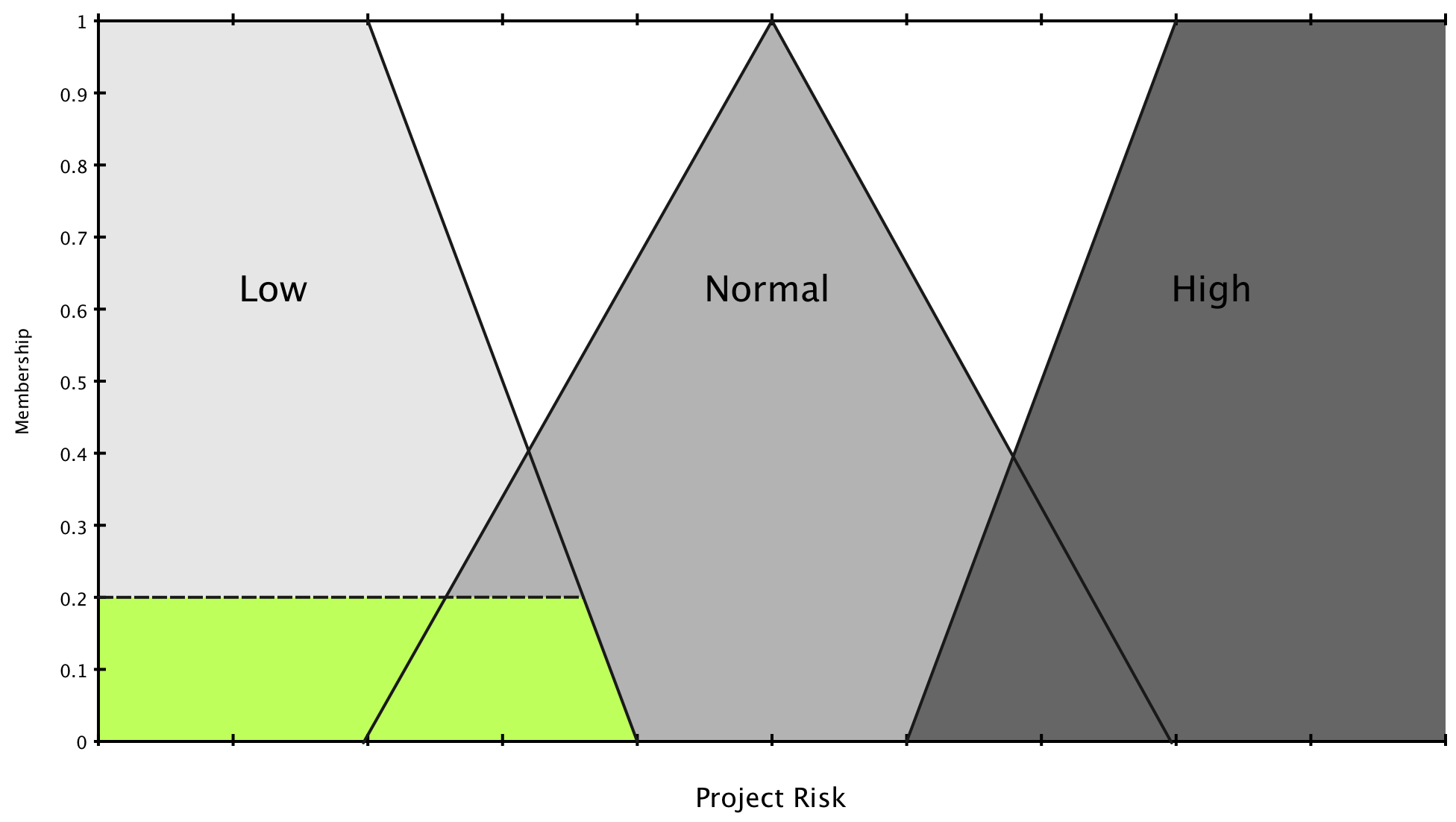
$$\mu_{\text{risk}=\text{normal}}(z) = 0.2$$
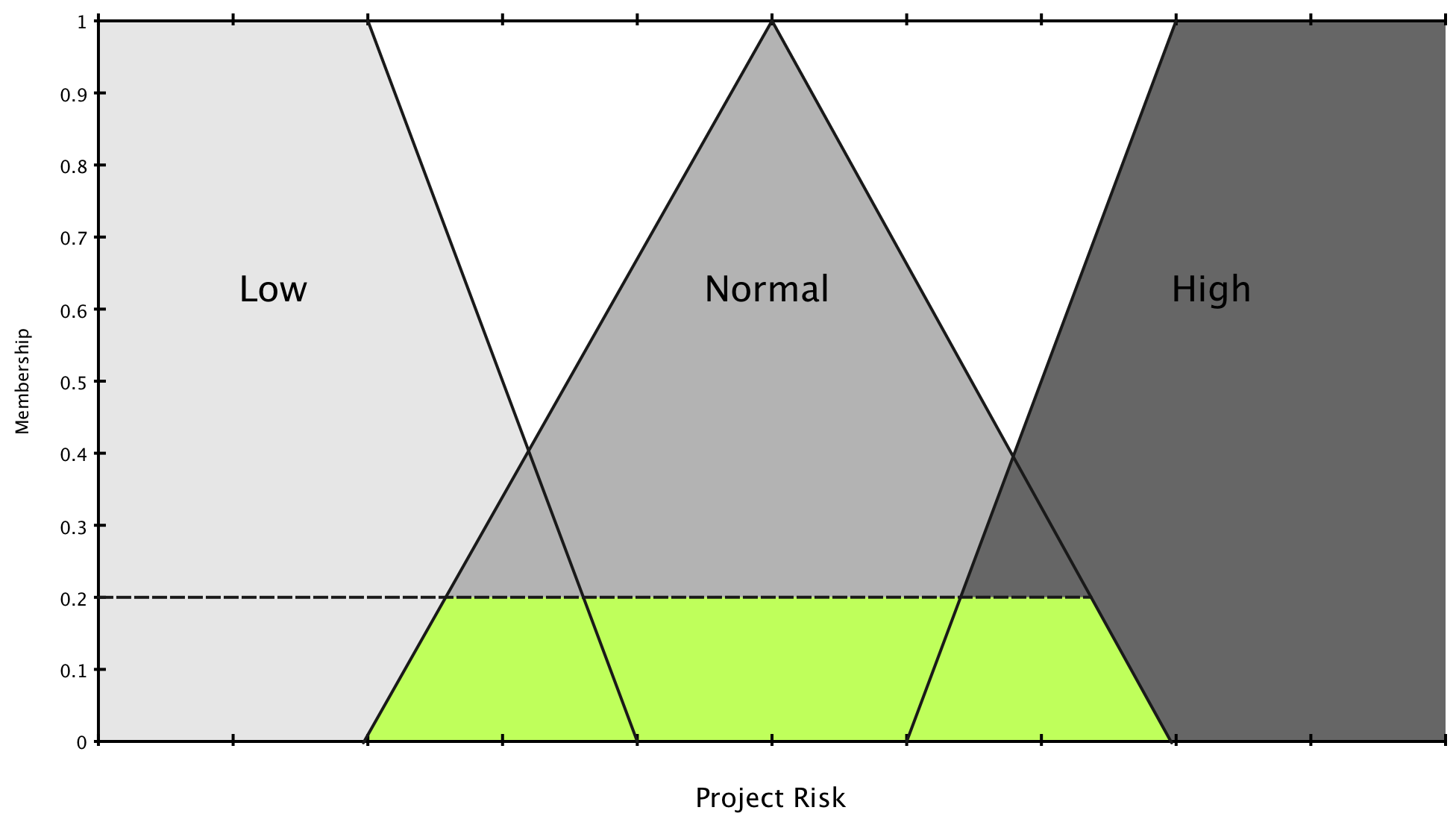
$$\mu_{\text{risk}=\text{high}}(z) = 0.5$$
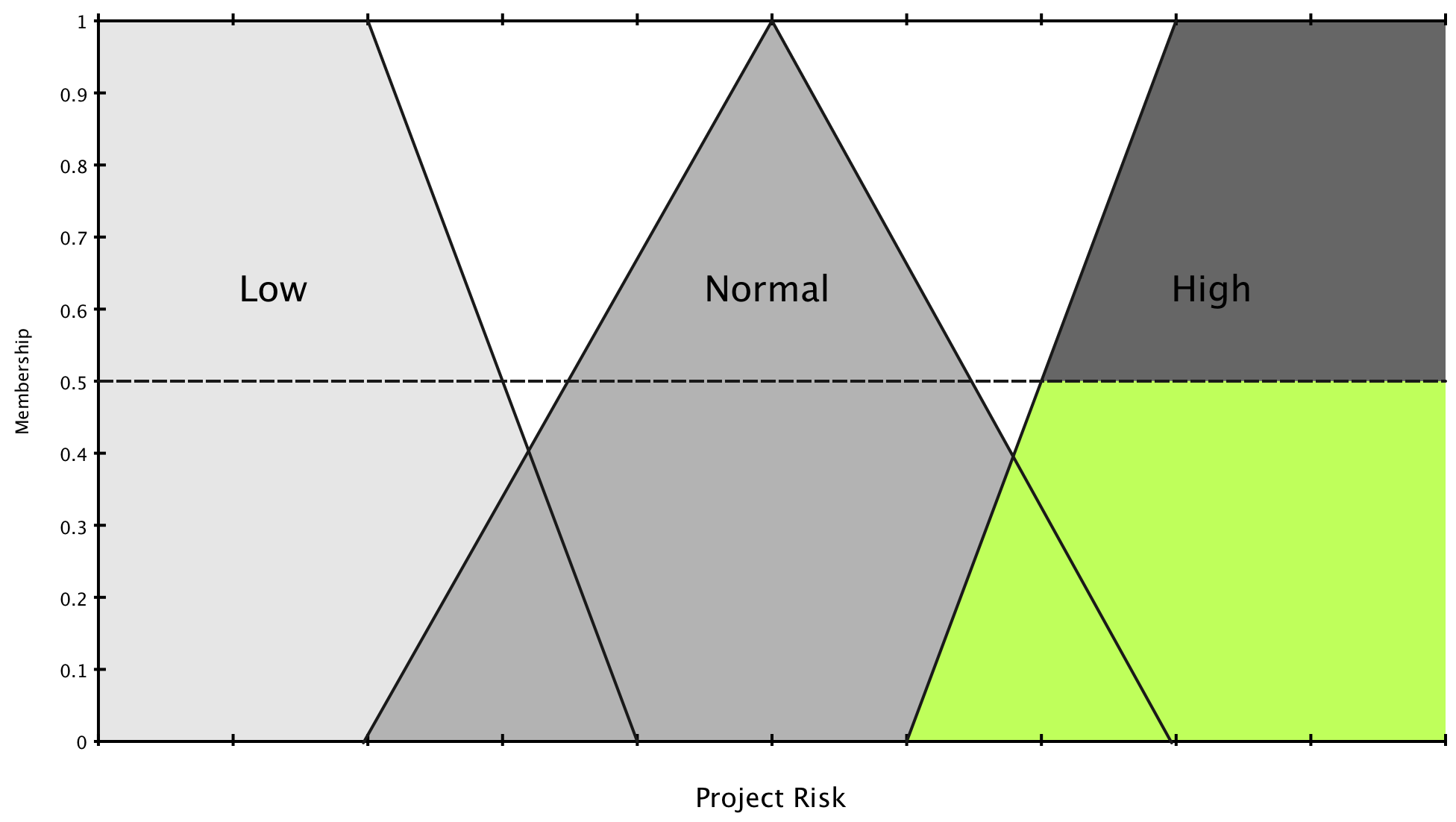
We perform a union on all of the scaled functions to obtain the final result. The result is again shown in green.
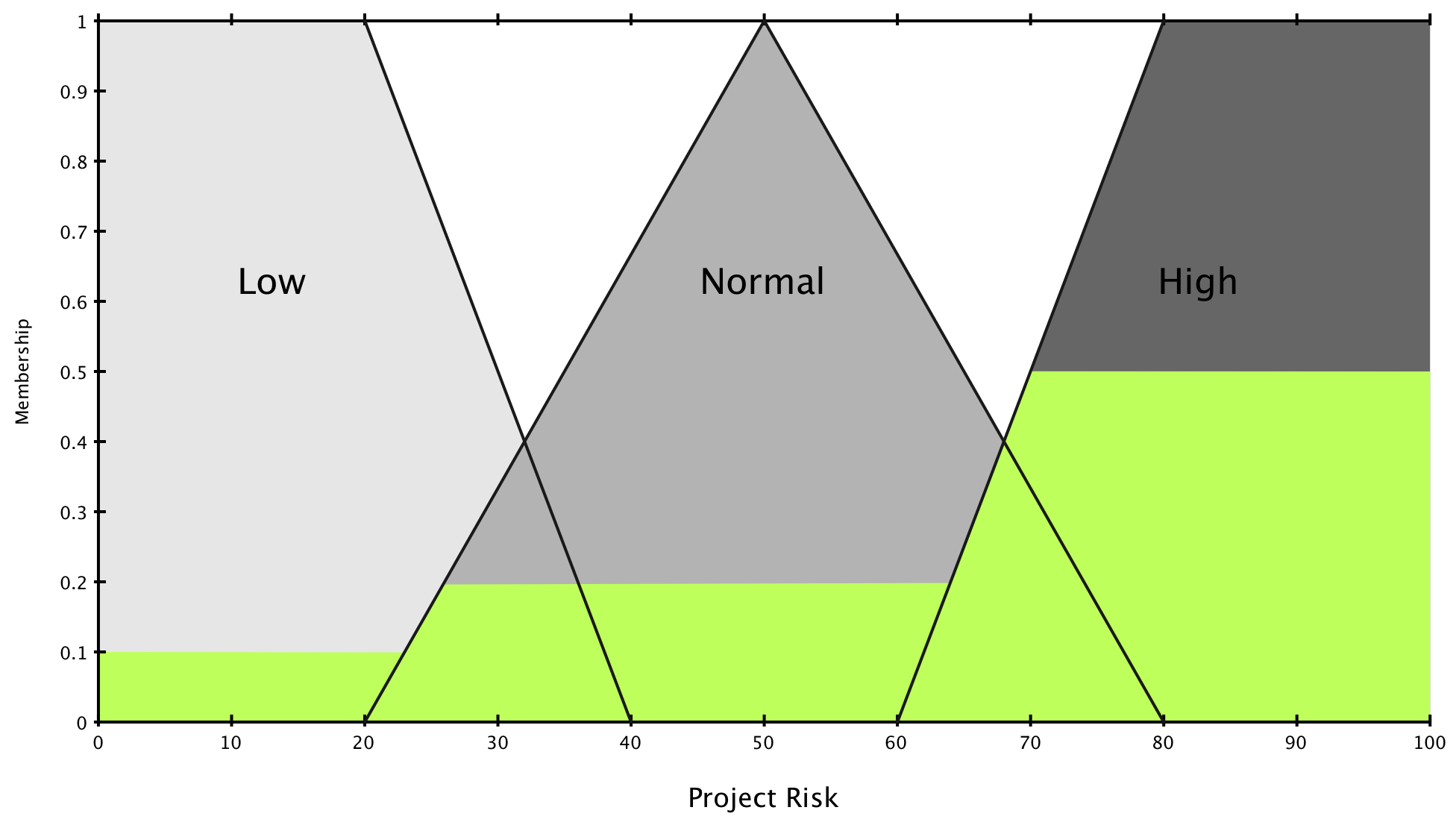
Defuzzification
The defuzzification can be performed in several different ways. The most popular method is the centroid method.
Centroid method Calculates the center of gravity for the area under the curve.
$$ COG = \frac{\sum_{x=a}^b \mu_A(\chi)x}{\sum_{x=a}^b \mu_A(\chi)} $$
Bisector Vertical line that divides the region into two sub-regions of equal area. It is sometimes, but not always, coincident with the centroid line. Mean of maximum Assuming there is a plateau at the maximum value of the final function take the mean of the values it spans. Smallest value of maximum Assuming there is a plateau at the maximum value of the final function take the smallest of the values it spans. Largest value of maximum Assuming there is a plateau at the maximum value of the final function take the largest of the values it spans.
We chose the centroid method to find the final non-fuzzy risk value associated with our project. This is shown below.
$$ COG = \frac{(0 + 10 + 20)*0.1 + (30 + 40 + 50 + 60)*0.2 + (70 + 80 + 90 + 100)*0.5}{(0.1 * 3) + (0.2 * 4) + (0.5 * 4)} = 67.4 $$
The result is that this project has 67.4% risk associated with it given the definitions above.